HashMap源码（五）—— 底层红黑树原理解析(新增)动图分析

满足红黑书结构原则：

• 每个节点只能是红色或者黑色
• 根节点都是黑色
• 不可能有连在一起的红色节点
• 每个红色节点的两个子节点都是黑色，叶子节点都是黑色
• 除了根节点，插入的时候每个节点都是红色

红黑树示例图：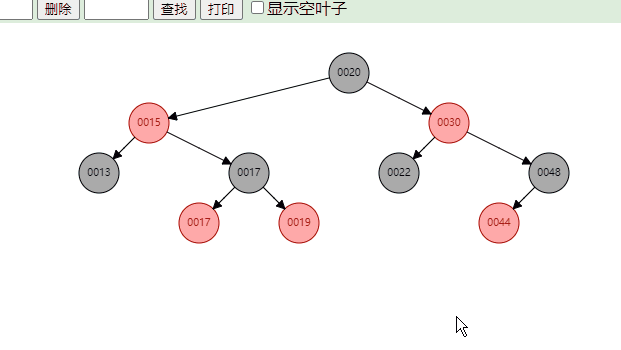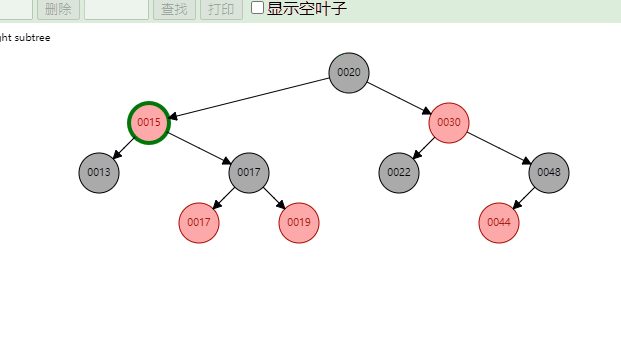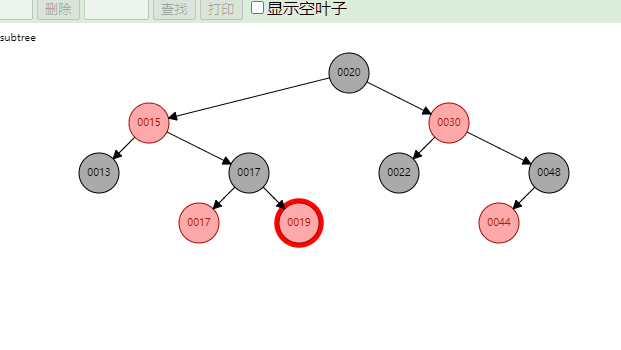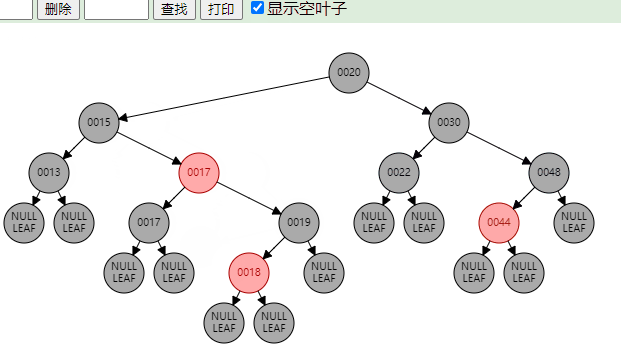

HashMap底层为什么要用红黑树不用完全平衡二叉树（AVL数）：

红黑树：黑色完美平衡，任意一个节点到每个叶子节点的路径都包含想通数量的黑色节点。

AVL树和红黑树有几点比较和区别：

• （1）AVL树是更加严格的平衡，因此可以提供更快的查找速度，一般读取查找密集型任务，适用AVL树。
• （2）红黑树更适合于插入修改密集型任务。
• （3）通常，AVL树的旋转比红黑树的旋转更加难以平衡和调试。

新增节点时红黑树旋转和颜色变换规则：

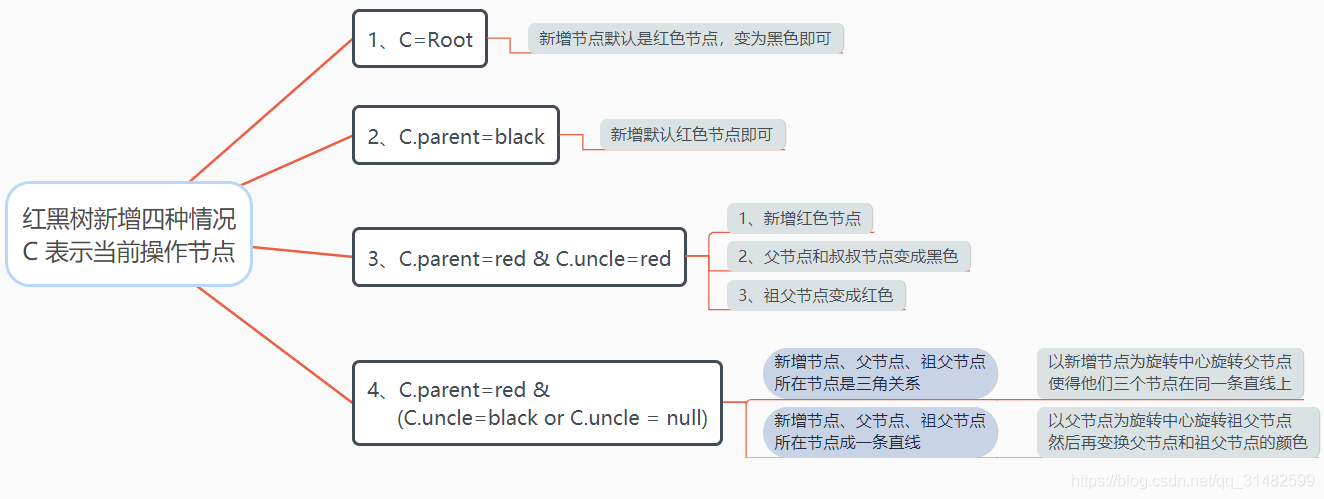
变色的情况：当前结点的父亲是红色，且他的祖父节点的另一个子节点（叔叔节点）也是红色：

• a、把父节点设置为黑色
• b、把叔叔节点也设置为黑色
• c、把父亲的父节点（祖父节点）设置为红色
• d、把指针定义到祖父节点设为当前要操作的节点，目的是为了平衡修改颜色其它节点不满足红黑树原则的情况（通过更改颜色或左旋右旋平衡，以此类推）
• 颜色变换示例 (给0005新增一个大于它的子节点)：
  

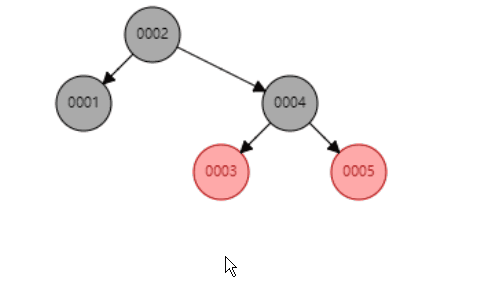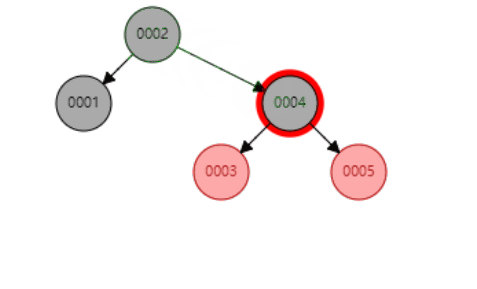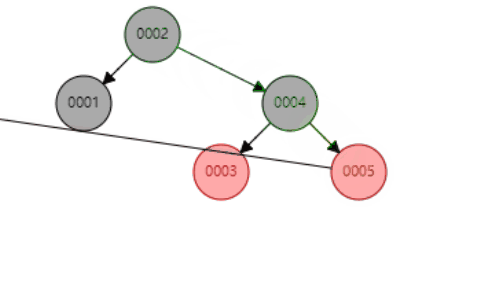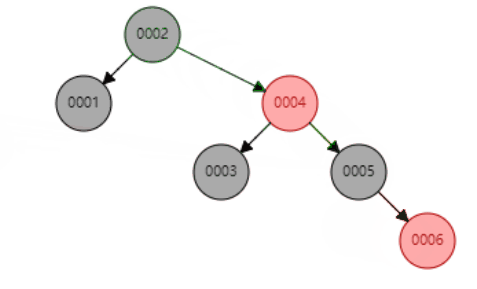
旋转示例（新增节点、父节点、祖父节点同一条直线）

• a、以最短路径旋转(顺时针为右旋，逆时针为左旋)
• b、以父节点为旋转中心，旋转祖父节点
• c、父节点变成黑色，祖父节点变成红色
• d、当前操作节点为变成红色的祖父节点（递归他坐在的父节点是否满足红黑树原则）
• 旋转示例（新增节点5，以父节点4为旋转中心旋转祖父节点，该示例为左旋操作）
  

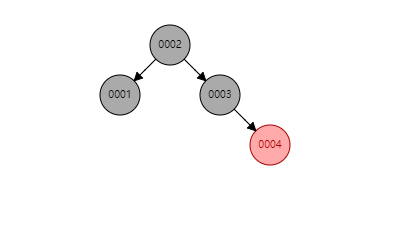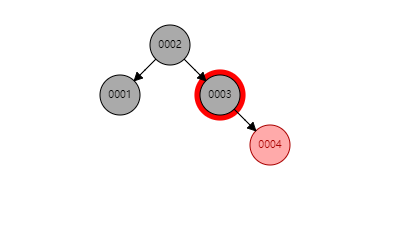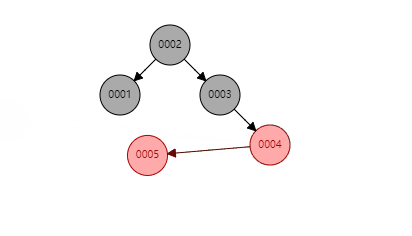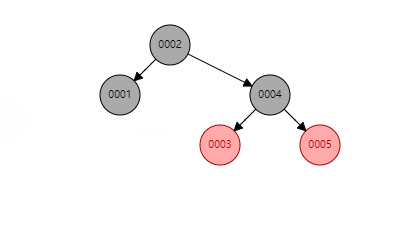
旋转示例（新增节点、父节点、祖父节点同呈三角关系）

• a、以最短路径旋转(顺时针为右旋，逆时针为左旋)
• b、首先以新增节点为旋转中心，旋转父节点，使新增节点、父节点、祖父节点在同一条直线上
• c、然后再参考上面同一条直线的情况进行旋转（递归处理，以此类推）
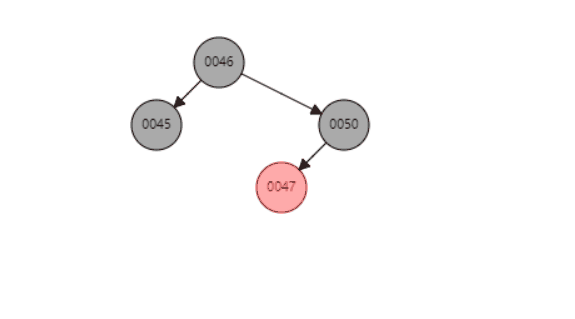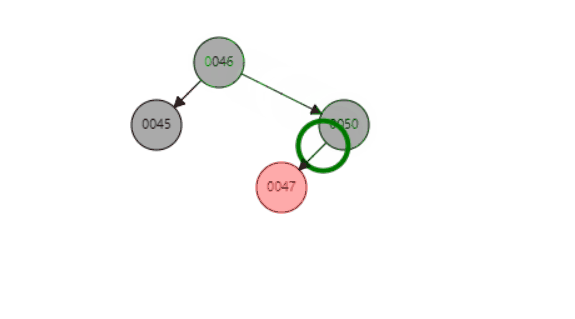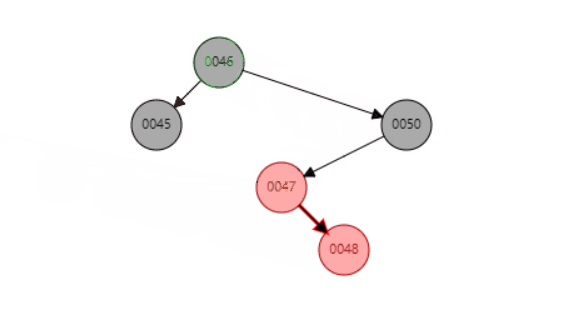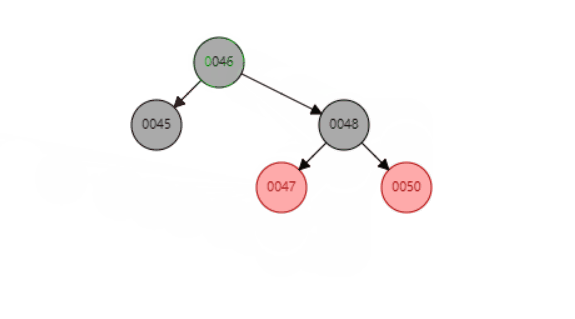
• 旋转示例：
  1. 新增节点48，以48为圆心旋转47节点——左旋
  2. 然后变成在同一条线上的情况，以48为圆心，旋转父节点50——右旋
     

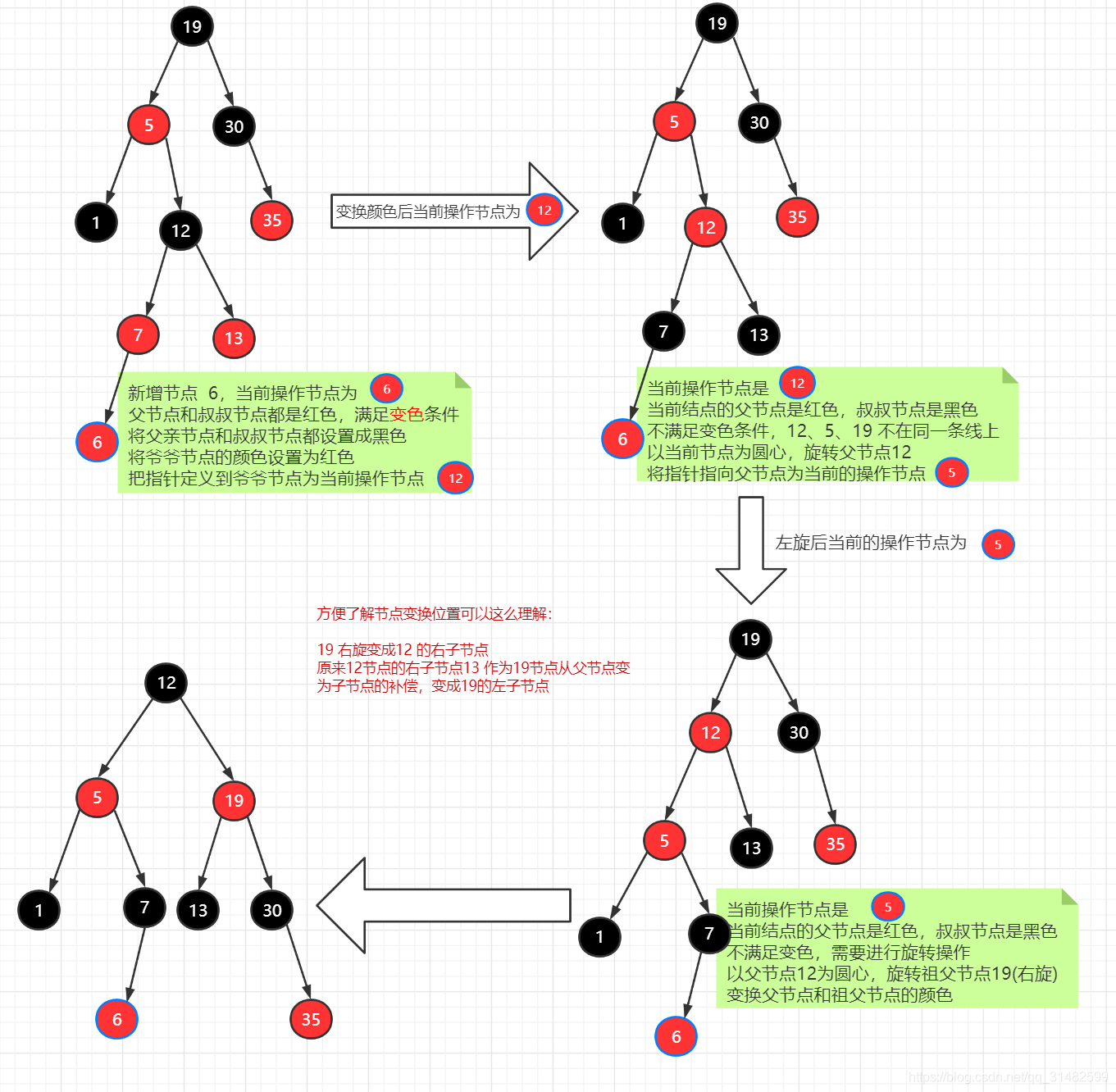
红黑树详细变换图解

HashMap红黑树源码分析

treeify()方法介绍

之前有介绍到 treeifyBin()，将普通节点转化成树节点，

再根据treeify()方法转换成红黑书结构

final void treeify(Node<K,V>[] tab) {
            TreeNode<K,V> root = null;  // 根节点
            for (TreeNode<K,V> x = this, next; x != null; x = next) {
                next = (TreeNode<K,V>)x.next;
                x.left = x.right = null;
                if (root == null) {      //新增节点为根节点时，无父节点，根节点是黑色
                    x.parent = null;
                    x.red = false;
                    root = x;
                } else {
                    K k = x.key;
                    int h = x.hash;
                    Class<?> kc = null;   //key 所属Class
                    for (TreeNode<K,V> p = root;;) { 
                        int dir, ph;      //dir 标识方向 -1，向左子树走   1 向右子树走     当前结点的hash值
                        K pk = p.key;
                        if ((ph = p.hash) > h)  //下一个节点小于当前结点时  向左走
                            dir = -1; 	 //向左子树走
                        else if (ph < h)
                            dir = 1;    //右
                        else if ((kc == null &&           //hash相等的情况
                                  (kc = comparableClassFor(k)) == null) ||
                                 (dir = compareComparables(kc, k, pk)) == 0)    // 如果key实现了compareable接口，并且是相同的Class实例，通过compare 比较两者
                            dir = tieBreakOrder(k, pk); //最后通过tieBreakOrder 进行比较
                        TreeNode<K,V> xp = p;  
                        // 找到符合条件的，根据 dir 的值，并将新节点设置为子节点  
                        if ((p = (dir <= 0) ? p.left : p.right) == null) {
                            x.parent = xp;  
                            if (dir <= 0)
                                xp.left = x;
                            else
                                xp.right = x;
                             // 重新平衡红黑树节点
                             // 根据不同情况对节点进行变色、左旋、右旋（左旋右旋就是改变当前结点、父节点、祖父节点的指针的一个过程）
                            root = balanceInsertion(root, x);
                            break;
                        }
                    }
                }
            }
            //如果HashMap元素数组根据下标取得的元素是一个TreeNode类型，
            //那么这个TreeNode节点一定要是这颗树的根节点，同时也要是整个链表的首节点。
            //把红黑书的根节点设置为所在槽的第一个元素
            moveRootToFront(tab, root);
        }

putTreeVal()方法

该方法是在HashMap进行put的时候，如果是树形结构的时候会调用putTreeVal方法

final TreeNode<K,V> putTreeVal(HashMap<K,V> map, Node<K,V>[] tab,
                                       int h, K k, V v) {
            Class<?> kc = null;
            //标识是否已经遍历过一次树，
            boolean searched = false;
            //找到根节点
            TreeNode<K,V> root = (parent != null) ? root() : this;
            for (TreeNode<K,V> p = root;;) {
            	// 方向-1、向左  1向右，当前节点hash，当前结点 K pk
                int dir, ph; K pk;
                if ((ph = p.hash) > h)
                    dir = -1;
                else if (ph < h)
                    dir = 1;
                else if ((pk = p.key) == k || (k != null && k.equals(pk)))
                	// 当hash值相等，直接返回节点   在外层方法对v进行覆盖写入
                    return p;
                // key的 hash相等   key的value不等 的情况 
                else if ((kc == null &&
                          (kc = comparableClassFor(k)) == null) ||
                         (dir = compareComparables(kc, k, pk)) == 0) {
                    /**
                     * 看是否能够得到那个键对象equals相等的的节点
                     * 如果得到了键的equals相等的的节点就返回
                     * 如果还是没有键的equals相等的节点，那说明应该创建一个新节点了
                     */
                    if (!searched) {
                        TreeNode<K,V> q, ch; 
                        searched = true;  // 标识已经遍历过次
                        // 递归查找对应hash形同key value不等的节点
                        if (((ch = p.left) != null &&
                             (q = ch.find(h, k, kc)) != null) ||
                            ((ch = p.right) != null &&
                             (q = ch.find(h, k, kc)) != null))
                             //找到后直接返回，外层方法进行写入
                            return q;
                    }
                    // 到这儿的时候，没有找到相等hash 相同equels 的hash
                    // 在比较当前结点和指定key键的大小，得到 下一个节点的方向（左还是右）
                    dir = tieBreakOrder(k, pk);
                }
                TreeNode<K,V> xp = p;
                // 根据dir 找到左子节点或者右子节点不为空的节点
                // 创建一个新的树节点，当前结点和父节点相关的关系属性
                if ((p = (dir <= 0) ? p.left : p.right) == null) {
                    Node<K,V> xpn = xp.next; // 获取当前结点的next节点
                    TreeNode<K,V> x = map.newTreeNode(h, k, v, xpn);  // 创建新节点
                    if (dir <= 0)
                        xp.left = x; // dir=-1 时，标识向左   将当前结点的左子节点设置成新增的新节点
                    else
                        xp.right = x; // dir=1的情况  
                    xp.next = x; //将新节点设置成当前结点的下一个节点
                    x.parent = x.prev = xp; //设置新节点的parent 和prep 均是当前结点
                    if (xpn != null)
                        ((TreeNode<K,V>)xpn).prev = x; //如果原来的next节点不为空，那么原来的next节点的前节点指向到新的树节点
                    // 重新平衡，以及新的根节点置顶
                    moveRootToFront(tab, balanceInsertion(root, x));
                    return null; //返回null 标识产生了一个新节点
                }
            }
        }