HashMap源码(七)—— 红黑树删除原理分析 动态图解析
红黑书的删除本质上是一个穷举的过程
删除情况说明
删除的节点没有子节点的情况
- 如果为红色,直接删除即可,不会影响黑色节点的数量
- 如果为黑色,删除的时候需要进行平衡操作
删除的节点只有一个子节点时,删除节点只能是黑色,子节点也只能是红色。否则无法满足红黑树黑色节点完全平衡的特性(从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点)
如果删除节点有两个子节点时,使用后继节点作为替换的删除节点,然后再按照前面两种情况处理
删除情况具体分析
删除的节点没有子节点(非null节点)的情况
a、如果为红色,直接删除即可,不会影响黑色节点的数量
删除红色节点(13)示例(不影响黑色节点数量,不需要平衡操作)
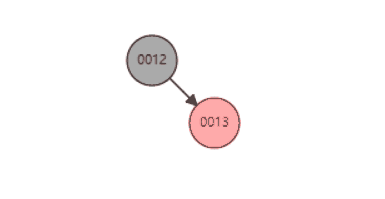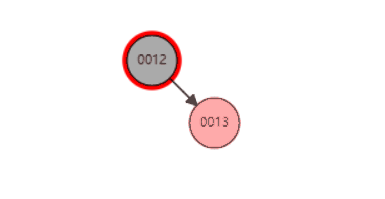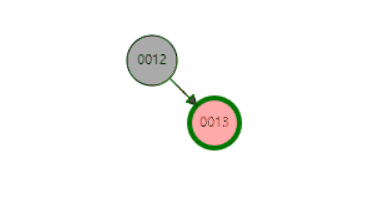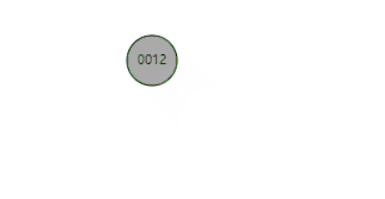
b、如果为黑色,删除的时候需要进行平衡操作
删除示例,删除节点11(平衡操作后面会介绍到)
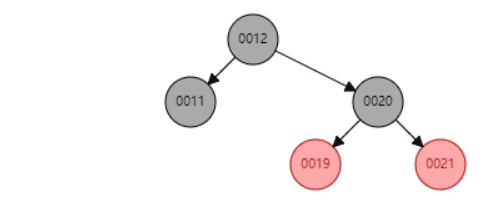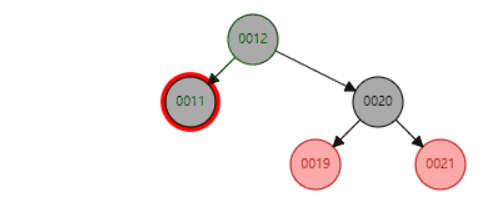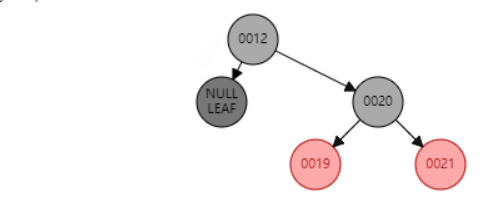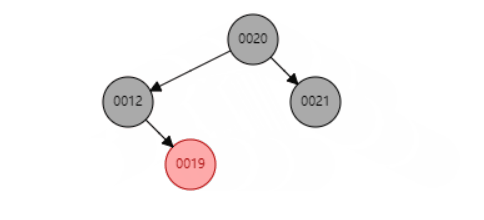
删除的节点只有一个子节点时,删除节点只能是黑色,子节点也只能是红色。
为什么该情况下,删除节点只能是黑色,子节点只能是红色,如图所示: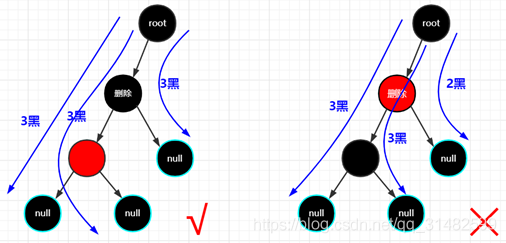
1 | |
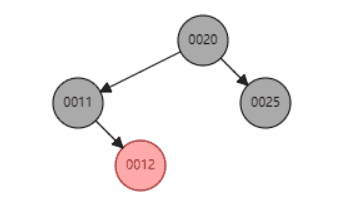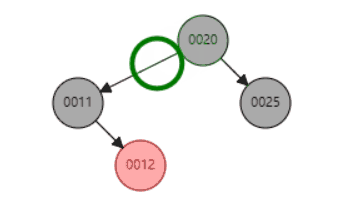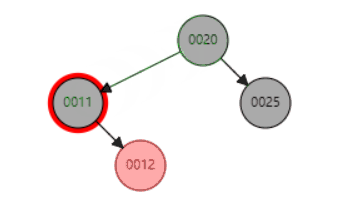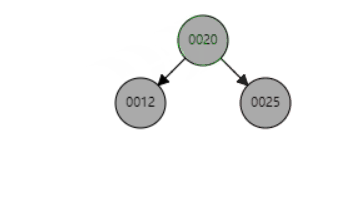
删除节点动态示例,删除节点11(分别是含左子树和右子树的情况):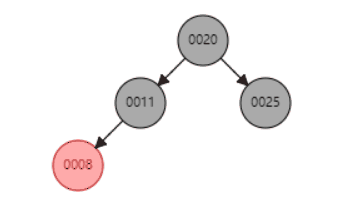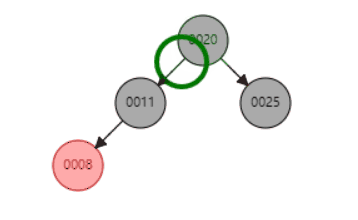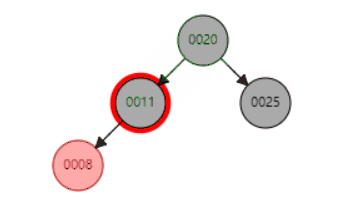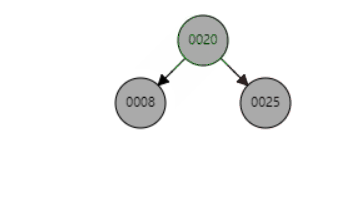
如果删除节点有两个子节点时,使用前驱节点或后继节点作为替换的删除节点,然后再按照前面两种情况处理(本文示例以前驱节点为例)
1 | |
下面演示示例只演示其中一种,大概了解一下变化规则。具体的平衡逻辑在后面会介绍到。
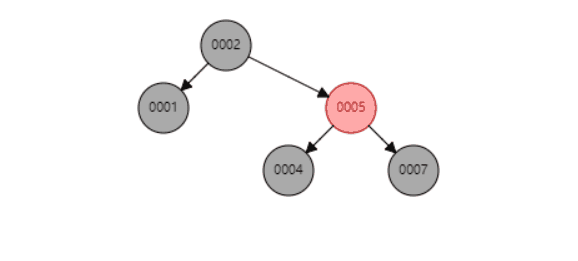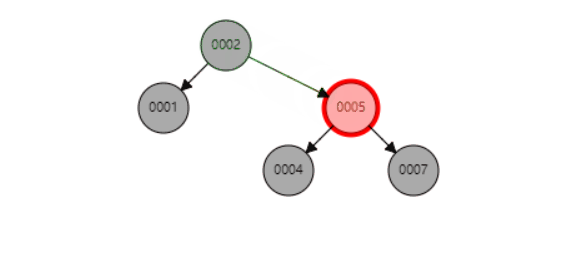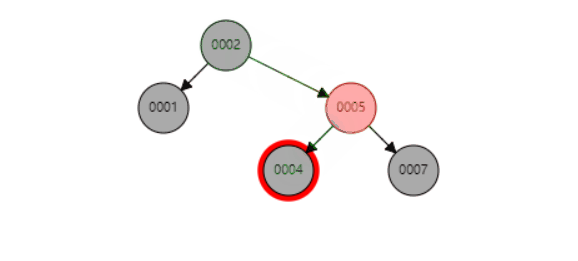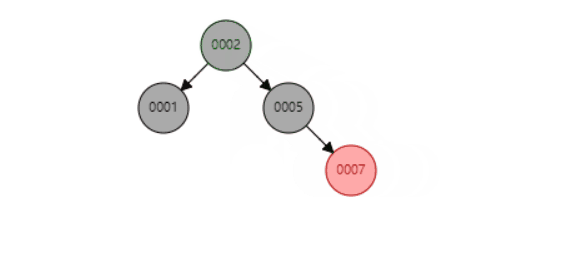
比如删除节点100,首先会找到前驱节点60,然后替换内容后,将后继节点删除。即将删除情况转变成上面介绍到的两种情况。删除完成后,再做节点平衡操作(后面会介绍具体平衡细节)。
删除示例,删除100节点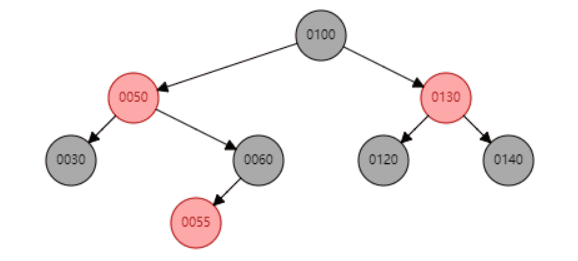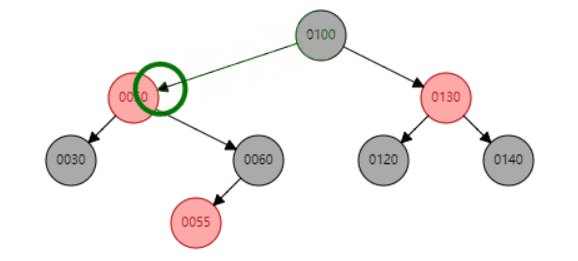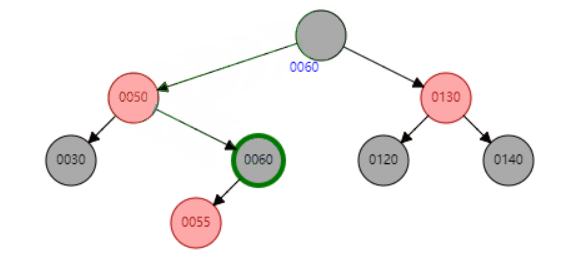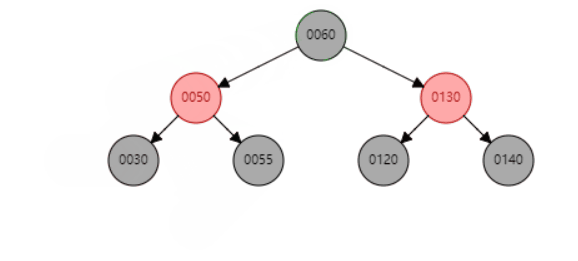
红黑树删除平衡情况分析
前面分析的三种情况,1.a 和 2 这两种情况下删除比较简单,不需要做红黑树节点平衡操作,而 3 这种情况之前也分析了,通过用前驱节点或者后继节点替换被删除的节点,将删除情况转换成1、2这种情况然后再删除,又由于1.a 和 2 不需要进行平衡处理,所以后面删除平衡操作主要围绕1.b的情况分析。
首先为了方便后面的描述,对节点进行一个名称的约束,如下图所示: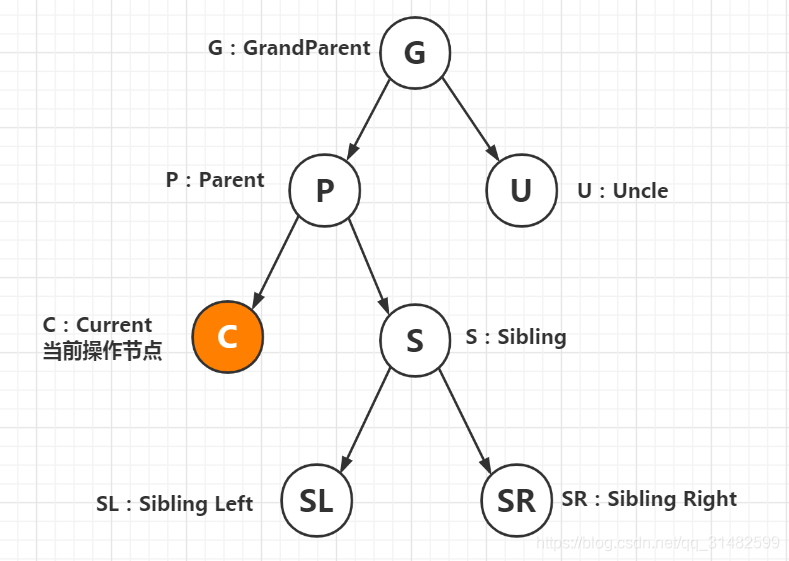
对于删除平衡操作也是一个穷举的过程(删除黑色节点引起的平衡问题)
1 | |
以下内容是删除的节点找到的前驱节点是没有子节点的黑色节点的情况(也就是删除删除黑色叶子节点的情况)
a、S 是黑色的情况
a、当 P 是 红 色 \color{red}{当P是红色}当P是红色,SL和SR是 NULL 时,删掉节点4
删掉节点4后,P变黑色,S变红色即可完成黑色节点平衡。
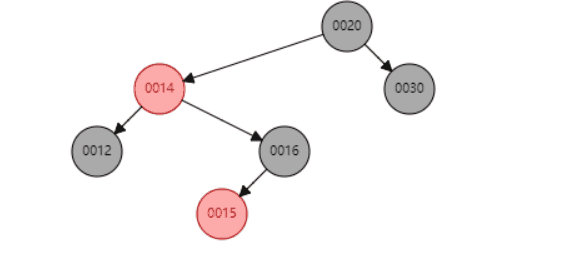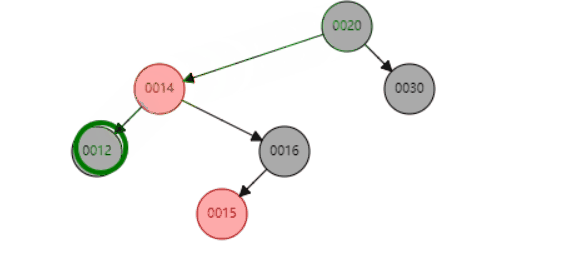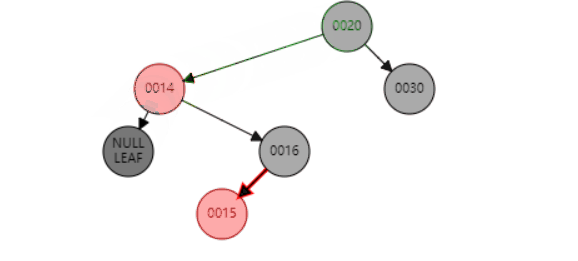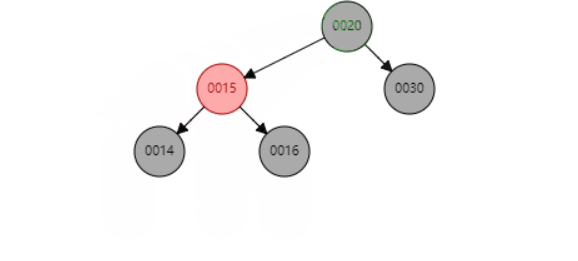
b、当P是红色,SL是红色,SR是NULL
删除节点12,因为删除的是黑色节点,SL又是红色的节点,可以利用这个红色节点补充删除的黑色节点达到局部黑色节点平衡。
先已SL为圆心,右旋S节点,更改SL和S的颜色
再已SL为圆心,左旋P节点,再次更改P和SL节点的颜色即可
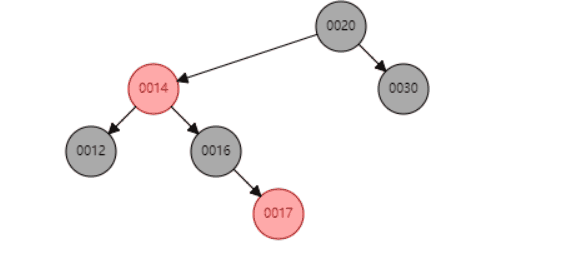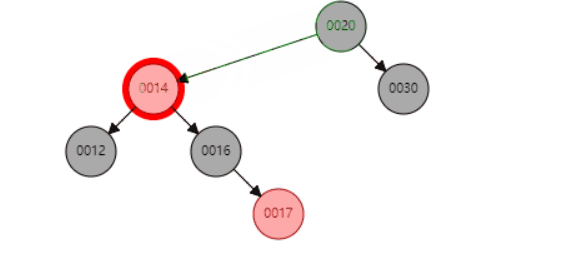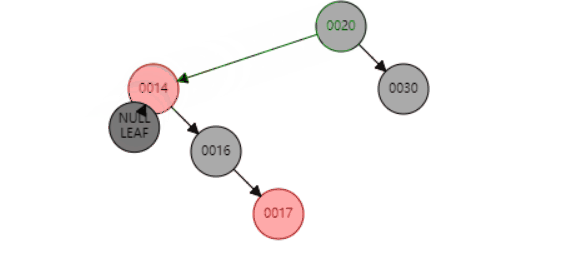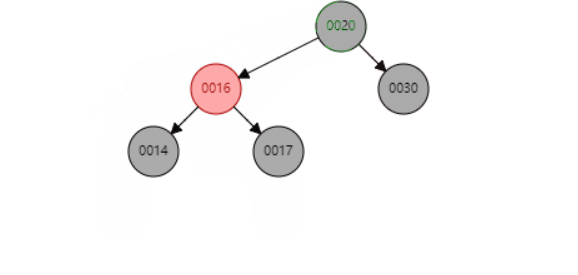
c、当P是红色,SL是null,SR是红色
类似上面一种场景
删除节点14后
以S为圆心,左旋P节点 即可达到平衡操作
d、当P是黑色,SL是null,SR是null
由于删除的是一个黑色节点,并且相邻兄弟节点没有红色节点
所以在删除后左侧这一块是不可能平衡,就会影响到叔叔节点的颜色
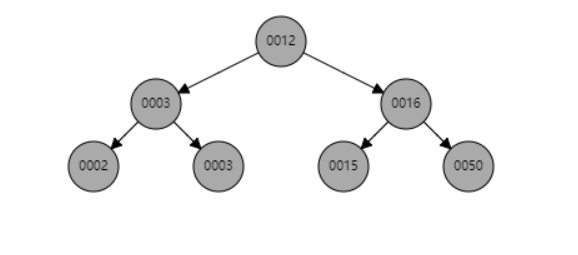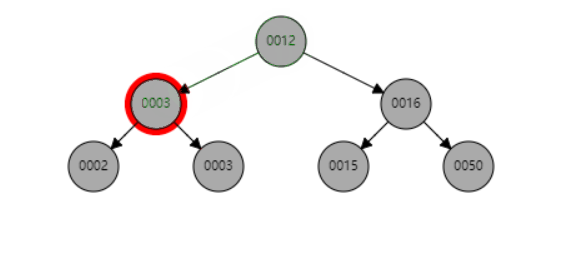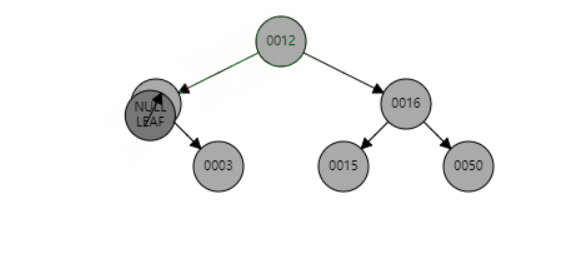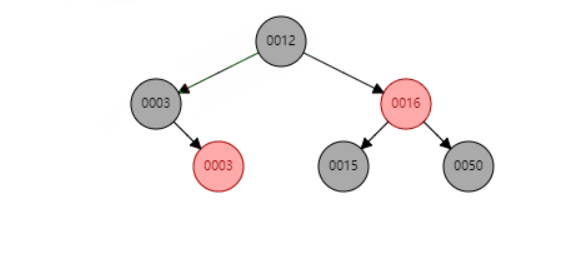
e、当P是黑色,SL是红色,SR是null
删除节点16 后,已SL为圆心,右旋S 节点,SL和S均变色然后再以SL为原型左旋P节点 最终三个节点的颜色都变成黑色
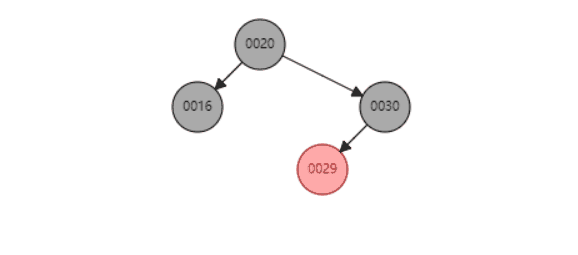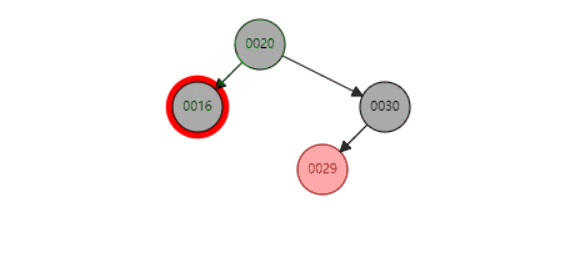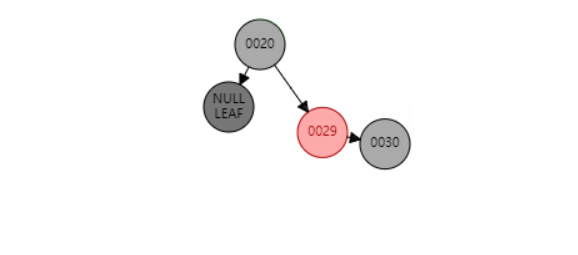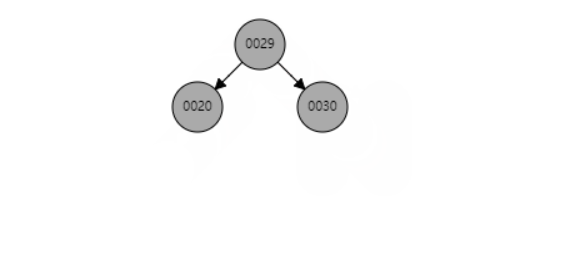
f、当P是黑色,SL是null,SR是null红色
同上面类似,以S为圆心,左旋P节点 最后都红色节点变成黑色节点即可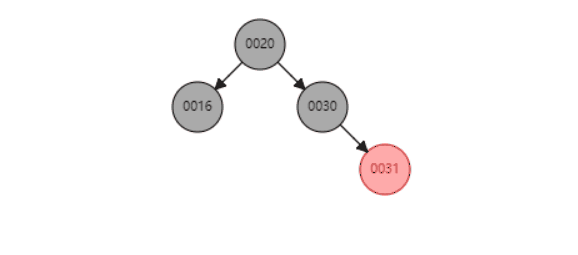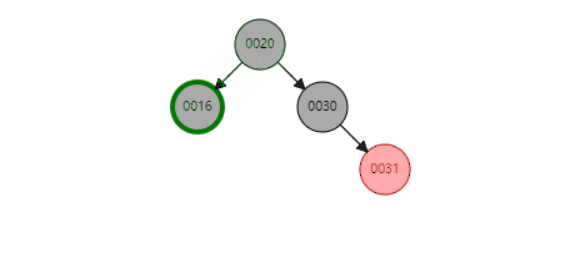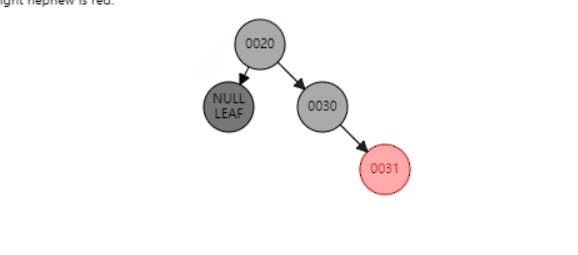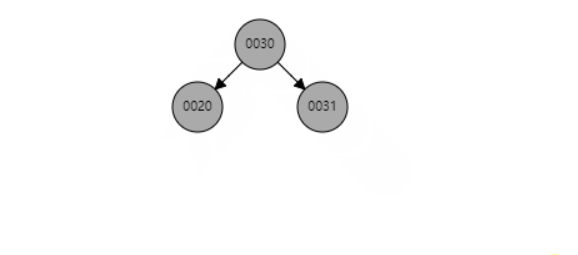
S 是红色的情况
和上面类似
具体变化细节可以用下面的网站工具实践:
http://www.u396.com/wp-content/collection/data-structure-visualizations/RedBlack.html
保持平衡的原则就是节点的每个分支的黑色节点数是相同的
HashMap红黑树删除源码分析
remove方法
1 | |
removeNode 方法
1 | |