力扣【LeetCode】—— 189. 旋转数组【java】
题目链接:https://leetcode-cn.com/problems/rotate-array/
题目:
给定一个数组,将数组中的元素向右移动 k 个位置,其中 k 是非负数。
示例:
[1,2,3,4,5,6,7] 和 k = 3
结果:
[5,6,7,1,2,3,4]
说明:
尽可能想出更多的解决方案,至少有三种不同的方法可以解决这个问题。
要求使用空间复杂度为 O(1) 的 原地 算法。
方案一:暴力
该解决方案虽然满足题意中的空间复杂度条件,但是时间复杂度为O(k*n),
1
2
3
4
5
6
7
8
9
10
11public void rotate(int nums[], int k) {
k = k % nums.length;
for (int j = 0; j < k; j++) {
int pre = nums[nums.length - 1];
for (int i = 0; i < nums.length; i++) {
int curr = nums[i];
nums[i] = pre;
pre = curr;
}
}
}时间复杂度 O (k*n),k 次n个元素的遍历
空间复杂度 O (1) ,无额外空间占用
像这种暴力解决方案一般不是题目的解决方案。而题目中有说明至少有三种不同方法可以解决这个问题,所以还应该有其他的解决思路,本文列举了如下几种另外的解决思路
方案二:引入额外数组
该方式和前面暴力解题方式是最简单的解题思路,但是不满足题目条件,题目中有说明用空间复杂度为O(1) 的原地算法,而这种解题方案的空间复杂度为O(n),故不满足要求
1
2
3
4
5
6
7
8
9
10public void rotate(int[] nums, int k) {
int[] arr = new int[nums.length];
for(int i = 0; i <nums.length;i++){
arr[(i+k)%nums.length] = nums[i];
}
// nums = arr;
for(int i = 0; i < nums.length; i++) {
nums[i] = arr[i];
}
}时间复杂度:O(n)
空间复杂度:O(n)
方案三:环状替换
个人觉得该方案也是最不好理解的一种方案
环状替换主要考虑两种情况,一种是数组长度是奇数的情况,这种情况下,形成环的方式只有一种。另一种情况也就是长度是偶数的情况,会形成多个环的情况,具体可以参考:https://leetcode-cn.com/problems/rotate-array/solution/xuan-zhuan-shu-zu-yuan-di-huan-wei-xiang-xi-tu-jie/ 如下截图来自该链接。
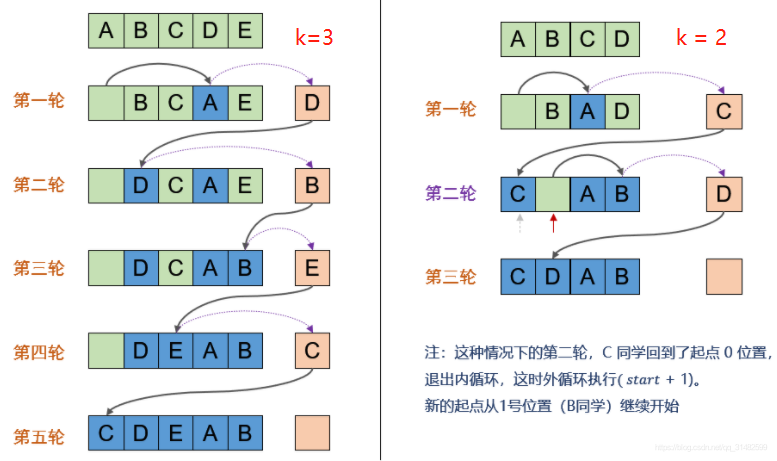
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17public void rotate(int nums[], int k) {
k %= nums.length;
int count = 0; // 移动总数
for (int start = 0; count < nums.length; start++) {
// currIndex 要移动元素位置
int currIndex = start;
int move = nums[currIndex]; // 要移动的元素
do {
int byReplaceIndex = (currIndex + k) % nums.length; // 被替换元素位置
int byReplace = nums[byReplaceIndex]; // 被替换的元素
nums[byReplaceIndex] = move; // 将要移动的元素放在被替换元素的位置
move = byReplace; // 重新设置要移动的元素为被替换的元素
currIndex = byReplaceIndex; // 替换要移动的元素位置为当前被替换的位置
count++;
}while (start != currIndex);
}
}时间复杂度 O (n),
空间复杂度 O (1)
方案四:数组反转
数组反转这个思想是参考官网解题思路的,通过三次反转操作,很巧妙的完成该题目的解答。
1
2
3
4
5
6
7
8
9
10
11
12
13public void rotate(int[] nums, int k) {
k %= nums.length;
reverse(nums, 0, nums.length - 1);
reverse(nums, 0, k - 1);
reverse(nums, k, nums.length - 1);
}
public static void reverse(int nums[],int start,int end) {
while (start < end) {
nums[start] = nums[start] + nums[end];
nums[end] = nums[start] - nums[end];
nums[start] = nums[start++] - nums [end--];
}
}时间复杂度 O (n),
空间复杂度 O (1)