二进制中模、原码、反码、补码分析和二进制位运算、移位运算

原码、反码、补码、模

二进制数

二进制数分为有符号数和无符号数。对于有符号位二进制数，最高位表示正负数，最高位1表示负数，最高位是0则表示正数。如一个8位的有符号位二进制数 1000 0001 最高是1则表示一个负数（-1） ，如果1000 0001 是无符号位，换算成十进制数是129.

模

指一个计量系统的计数范围，可以简单理解成一个范围，超出这个范围后回到原点，即一个轮回。模实质上是计量器产生”溢出”的量，它的值在计量器上表示不出来，计量器上只能表示出模的余数。任何有模的计量器可以将减法运算换算成加法运算。在同模下，互补的两个数相加等于模

例：时钟范围是1 ~ 12 ，即模为12

原码

原码就是我们看到的二进制的原始表示，符号位最高位是0 表示整数，1标识负数

例：
[+5]原 = 0000 0101
[-5]原 = 1000 0101

反码

正数的反码是本身，负数的反码是源码的最高位不变其余位取反

例：
[+5]反 = [0000 0101]反 = 0000 0101
[-5]反 = [1000 0101]反 = 1111 1010

补码

正数的补码是其本身，负数的补码是在反码的基础上 +1

例：
[+5]补 = [0000 0101]补 = 0000 0101
[-5]补 = [[1000 0101]反]+1 = [1111 1010]+1 = 1111 1011

为什么要有反码和补码

在计算机中，数据都是用补码的形式存储，没有反码原码的表示，只是方便理解提出的概念。计算机 CPU 的运算器只实现了加法器，而没有实现减法器。对于减法运算是通过加一个负数来计算的。利用高位溢出将减法运算变加法，即把两数相减看成是一个正数加上一个负数，把这两个数的补码相加，高位溢出(可以理解成舍掉模)，就实现了减法变加法。在计算机中，负数以其正值的补码形式表达。

• 验证
  如果使用整数加一个负数做减法运算时，计算的结果将不是我们所期待的结果

     如： 十进制中5-3=2 , 按照正常的逻辑减法变加法后为 5+(-3) ,计算如下
     0000 0101
     1000 0011 +
     ————————————————————
     0000 1000 --------> 8 (与期待值不符)

• 高位溢出，减法变加法的逻辑体验

  假设要将一个零点整的时钟 调整带到三点钟，有如下两种做法

  

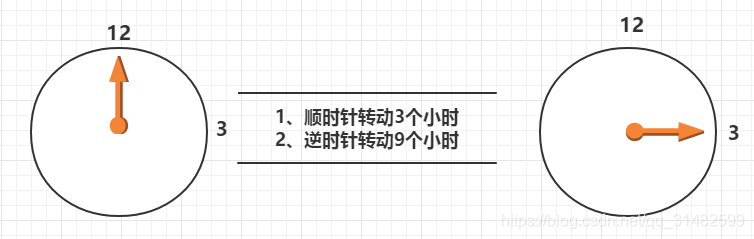
• 换算成十进制运算表示

  //12点钟按照0点计算
  0 + 3 = 3
  0 – 9 = 0+ (12-9)= 0 + (模-9) = 3   
  //按照12点计算
  12 + 3 = 15(舍去模12)= 3
  12 – 9 = 12 + (12-9) = 12 + 3 = 15(舍去模12) = 3 

  在二进制中，其方法完全一致，一个8位二进制最大数是1111 1111，如果再加1 则为 1 0000 0000 ,舍掉最高位则变成0000 0000 。所以8位二进制的模数为2的8次方，在计算机中也可以将减法问题化成加法问题，只需要把减数问题用相应的补数表示就可以，即补码。

  通过补码的方式计算 5-3 如下
     0101 --> 十进制5对应二进制的补码
  +  1101 –-> 十进制 -3 对应二进制的补码 
  ___________________________________________________________
    10010  -----> 舍去最高位为 0010   转换成十进制为2 (符合运算结果)

  所以在二进制中同样可以将一个减法运算通过补码的形式舍弃高位换算成加法运算

• 负数补码 = 反码+1 的分析：

  一个各个位都为1的数+1的值计算后会得到一个最高为为1其它位为0的二进制数，舍弃掉最高位即是0. 而我们又知道绝对值相等的两个正负数之和为0. 所以当指定一个二进制数后，应先找到与其相加后各个位的结果都为1的那个数（即反码），然后再用这个数加1 即找到这个数对应的相反数（补码）

二进制位运算

原码到补码的计算方式：取反+1，

补码到原码的计算方式：-1再取反。

序号	运算符	描述
1	&	按位与
2	l	按位或
3	^	按位异或
4	<<	左移
5	>>	右移
6	>>>	无符号右移

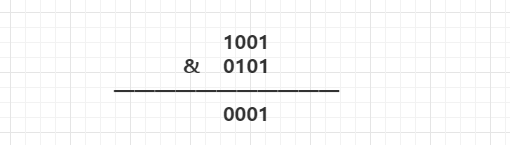
1. &：按位与

   只有当2个数对应的位都为1，该位运算结果为1，否则0。
   
   那么 9 & 5 = 1001 & 0101 = 0001 = 1
   

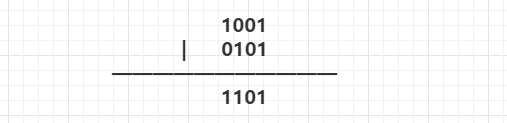
2. |：按位或

   只有当2个数对应的位有1，该位运算结果为1，否则0。
   
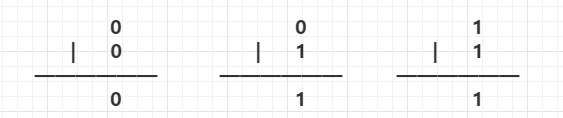
   那么 9 | 5 = 1001 | 0101 = 1101 = 13
   

3. ^：按位异或

   只有当2个数对应位的值不一样（“异”），该位运算结果为1，否则0。
   
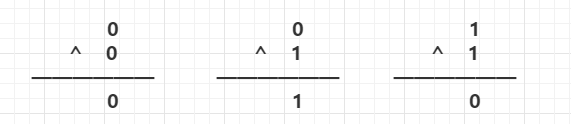
   那么 9 ^ 5 = 1001 ^ 0101 = 1100 = 12
   

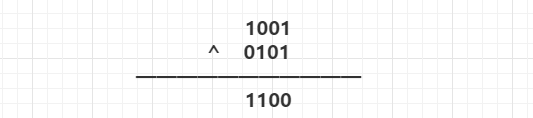
4. <<：左移

   将二进制的各个位全部左移指定位数，左边的丢弃，右边位补0

   正数：左移n位后的值等于原来值乘2n次方

   例：

   正数左移： 11 << 2
   
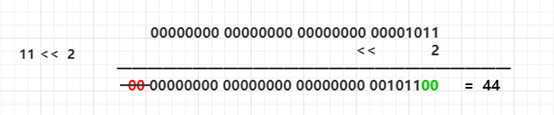
   负数左移：-11 << 2 （补码运算）
   

5. >>：右移

   将二进制的各个位全部右移指定位数，左边移空高位正数补0，负数补1，右边丢弃

   例：

   正数右移： 11>>2
   
   负数右移： -11>>2
   

6. >>>：无符号右移

   将二进制的各个位全部右移指定位数，左边移空位都0（不考虑正负），右边丢弃

   例：

   正数无符号右移：11 >>> 2
   
   负数无符号右移：-11 >>> 2
   
   验证结果
   

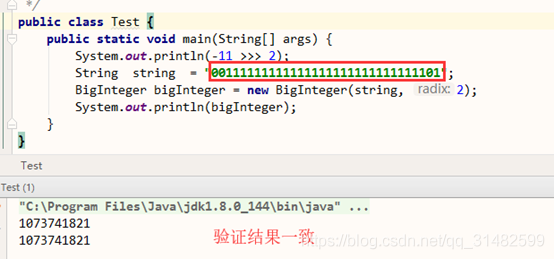
7. <<< (无该运算符)

   没有该运算符，同 << ,在左移运算中右面都是补0，没有符号位一说